Question

Find the equation of the axis of symmetry and the coordinates of the vertex of the graph of the function y = 2x2 + 4x –3

Answer 1

Your vertex would be (-1,-5)
and your axis of symmetry is x=-1

Answer 2

Axis of symmetry is x=-1.

The vertex of the graph is (-1,-5).

Explanation:

If a quadratic function is
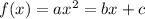`f(x)=ax^2=bx+c`, then the axis of symmetry is

`x=-(b)/(2a)`

`Vertex=(-(b)/(2a),f(-(b)/(2a)))`

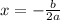
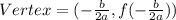
The given equation is

`y=2x^2+4x-3`

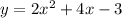
Here,

`a=2,b=4,c=-3`

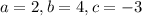
The axis of symmetry is

`x=-(4)/(2(2))=-1`

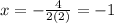
Substitute x=-1 in the given equation to find the y-coordinate of the vertex.

`y=2(-1)^2+4(-1)-3`

`y=2-4-3`

`y=-5`

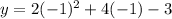
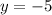
Therefore, the vertex of the graph is (-1,-5).