Question

If cos theta= -8/17 and theta is in quadrant 3, what is cos2 theta and tan2 theta

Answer 1

Answer:cos2θ= -161/289 and tan2θ= -240/161

Step-by-step explanation: I got this right on Edmentum

Answer 2

`\bf cos(\theta)=\cfrac{adjacent}{hypotenuse}\qquad \begin{array}{llll} \textit{now, hypotenuse is always positive}\\ \textit{since it's just the radius} \end{array} \\\\\\ thus\qquad cos(\theta)=\cfrac{-8}{17}\cfrac{\leftarrow adjacent=a}{\leftarrow hypotenuse=c}`

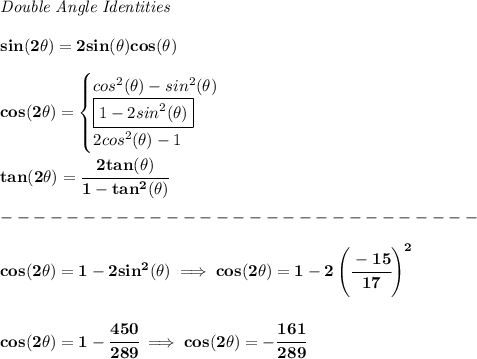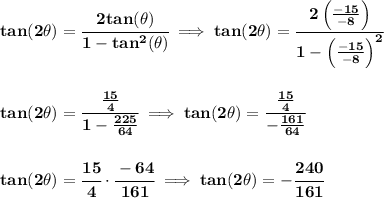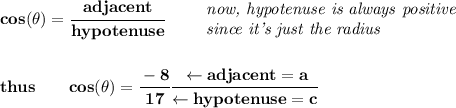
since the hypotenuse is just the radius unit, is never negative, so the - in front of 8/17 is likely the numerator's, or the adjacent's side

now, let us use the pythagorean theorem, to find the opposite side, or "b"


`\bf c^2=a^2+b^2\implies \pm√(c^2-a^2)=b\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite \end{cases} \\\\\\ \pm√(17^2-(-8)^2)=b\implies \pm√(225)=b\implies \pm 15=b`

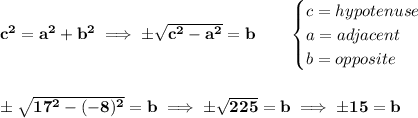
so... which is it then? +15 or -15? since the root gives us both, well
angle θ, we know is on the 3rd quadrant, on the 3rd quadrant, both, the adjacent(x) and the opposite(y) sides are negative, that means, -15 = b

so, now we know, a = -8, b = -15, and c = 17
let us plug those fellows in the double-angle identities then


`\bf \textit{Double Angle Identities} \\ \quad \\ sin(2\theta)=2sin(\theta)cos(\theta) \\ \quad \\ cos(2\theta)= \begin{cases} cos^2(\theta)-sin^2(\theta)\\ \boxed{1-2sin^2(\theta)}\\ 2cos^2(\theta)-1 \end{cases} \\ \quad \\ tan(2\theta)=\cfrac{2tan(\theta)}{1-tan^2(\theta)}\\\\ -----------------------------\\\\ cos(2\theta)=1-2sin^2(\theta)\implies cos(2\theta)=1-2\left( \cfrac{-15}{17} \right)^2 \\\\\\ cos(2\theta)=1-\cfrac{450}{289}\implies cos(2\theta)=-\cfrac{161}{289}`





`\bf tan(2\theta)=\cfrac{2tan(\theta)}{1-tan^2(\theta)}\implies tan(2\theta)=\cfrac{2\left( (-15)/(-8) \right)}{1-\left( (-15)/(-8) \right)^2} \\\\\\ tan(2\theta)=\cfrac{(15)/(4)}{1-(225)/(64)}\implies tan(2\theta)=\cfrac{(15)/(4)}{-(161)/(64)} \\\\\\ tan(2\theta)=\cfrac{15}{4}\cdot \cfrac{-64}{161}\implies tan(2\theta)=-\cfrac{240}{161}`