Question

Lamont’s grandmother started a stamp collection in 1914 (year 1) and added the same number of stamps to the collection each year. When Lamont’s mother received the collection in 1954, there were 203 stamps in the collection. Lamont’s mother continued to add the same number of stamps to the collection each year. When Lamont received the collection in 1990, there were 383 stamps in the collection. If Lamont continued to add the same number of stamps each year, how many stamps were in the collection at the end of 2000 (year 86)?

A. 204

B. 293

C. 433

D. 663

Answer 1

Answer: C. 433

Explanation:

Linear equation: y=mx+c, where m= constant rate of change, c=initial value of yor y-intercept.

Let x = number of years after 1914.

y= Number of stamps after x years.

In 1954 (year 40), there were 203 stamps in the collection.

i.e. 203=40m+c (i) [rate of change in number of stamps is constant]

In 1990 (year 76), there were 383 stamps in the collection.

i.e. 383=76m+c (ii)

Subtract (i) from (ii)

180= 36m

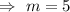`\Rightarrow\ m=5` i.e. 5 stamps added per year.

from (i),
`203=40(5)+c\Rightarrow\ c=203-200=3` [Initially he has 3 stamps]

Stamps in 2000(year 86) = m(86)+c= 5(86)+3

= 430+3

= 433

Hence, correct option is C. 433