Question

On top of a hill, a rocket is launched from a distance 80 feet above a lake. The rocket will fall into the lake after its engine burns out. The rocket's height, h, in feet above the surface of the lake, is given by the equation, h = -16t 2 + 64t + 80, where t is time in seconds. The maximum height of the rocket is

a0 feet.

Answer 1

Are you trying to find the maximum height? The time it will be to reach the maximum height? I'm pretty confused at what you need help with right now

Answer 2

Maximum height is 144 feet.

Explanation:

A quadratic equation y =
`ax^2+bx+c=0` gives maximum value when x =
`(-b)/(2a)`

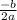
after finding the value of x we plug value of x in original equation in order to find the maximum value (minimum value in case of a >0)

on comparing given quadratic equation which is variable 't' ,we get a =-16 and b =64

t =
`(-64)/(2(-16))`

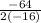
plugging this value of t =2 in original equation in order to get maximum value of h

so h =
`\-16(2)^2+16(2)+80`

which gives h =144 feet