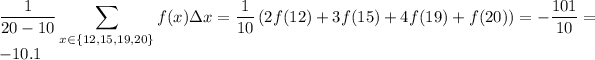Question

5. The function is continuous on the interval [10, 20] with some of its values given in the table above. Estimate the average value of the function with a Right Hand Sum Approximation, using the intervals between those given points. (4 points)

x 10 12 15 19 20
f(x) -2 -5 -9 -12 -16


A -9.250
B -10.100
C-7.550
D-6.700

Answer 1

-10.100

Explanation:

I just took this and the answer calculated above is correct

Answer 2

The average value of
`f(x)` over the given interval is


`\frac1{20-10}\displaystyle\int_(10)^(20)f(x)\,\mathrm dx`

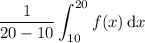
You're given five points, but only four will contribute to the sum as there are four subintervals that you can work with. Because you are finding the right-endpoint approximation, the height of the rectangles used in the Riemann sum will be determined by the points
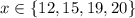
`x\in\{12,15,19,20\}`, where the height of each rectangle is the corresponding value of
`f(x)` and the width is the length of the subinterval. In this case, the lengths would be (left to right and respectively)
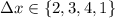
`\Delta x\in\{2,3,4,1\}`, which is simply the set of forward differences of the previous set.

So the average value is approximated by


`\frac1{20-10}\displaystyle\sum_{x\in\{12,15,19,20\}}f(x)\Delta x=\frac1{10}\left(2f(12)+3f(15)+4f(19)+f(20)\right)=-(101)/(10)=-10.1`