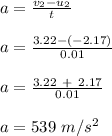Question

On a low-friction track, a 0.66-kg cart initially going at 1.85 m/s to the right collides with a cart of unknown inertia initially going at 2.17 m/s to the left. After the collision, the 0.66-kg cart is going at 1.32 m/s to the left, and the cart of unknown inertia is going at 3.22 m/s to the right. The collision takes 0.010 s.

What is the unknown inertia?
What is the average acceleration of the heavier cart?
What is the average acceleration of the lighter cart?

Answer 1

(a) the unknown inertia is 0.388 kg

(b) the average acceleration of the heavier cart is 317 m/s²

(c) the average acceleration of the lighter cart is 539 m/s²

Step-by-step explanation:

Given;

mass of the first cart, m₁ = 0.66 kg

initial speed of the first cart, u₁ = 1.85 m/s

let the mass of the cart with unknown inertia be m₂

initial velocity of the second cart, u₂ = 2.17 m/s to the left

velocity of the first cart after collision, v₁ = 1.32 m/s to the left

velocity of the second cart after collision, v₂ = 3.22 m/s

time of collision, t = 0.010 s

(a) What is the unknown inertia?

Apply the principle of conservation of linear momentum, to determine the unknown inertia.

let leftward direction be negative direction

let rightward direction be positive direction

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

0.66(1.85) + m₂(-2.17) = 0.66(-1.32) + m₂(3.22)

1.221 - 2.17m₂ = -0.8712 + 3.22m₂

1.221 + 0.8712 = 3.22m₂ + 2.17m₂

2.0922 = 5.39m₂

m₂ = 2.0922 / 5.39

m₂ = 0.388 kg

The unknown inertia is 0.388 kg

(b) the average acceleration of the heavier cart

the heavier cart has a mass of 0.66 kg

`a = (v_1 - u_1)/(t) \\\\a = (-1.32 - 1.85)/(0.01) \\\\a = -317 \ m/s^2\\\\|a| = 317 \ m/s^2`

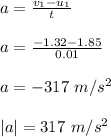
(c) the average acceleration of the lighter cart;

the lighter cart has a mass of 0.388 kg

`a = (v_2 - u_2)/(t) \\\\a = (3.22 - (-2.17))/(0.01) \\\\a =(3.22 \ +\ 2.17)/(0.01) \\\\a= 539\ m/s^2`