Consider the function
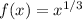
, which has derivative
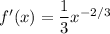
.
The linear approximation of

for some value

within a neighborhood of
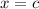
is given by
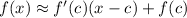
Let
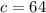
. Then
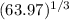
can be estimated to be
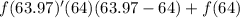
![\sqrt[3]{63.97}\approx4-(0.03)/(48)=3.999375](https://img.qammunity.org/2018/formulas/mathematics/high-school/pfb25g25bgub7p88sxnrydaszggq8nerkm.png)
Since
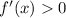
for
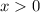
, it follows that

must be strictly increasing over that part of its domain, which means the linear approximation lies strictly above the function

. This means the estimated value is an overestimation.
Indeed, the actual value is closer to the number 3.999374902...