Question

Suppose 16% of the listeners of a radio station listen to it while they are at work. What is the approximate standard deviation of the sampling distribution of the proportion for the sample of size 72

Answer 1

so it's 4.3%?

Explanation:

Answer 2

Answer with explanation:

Sample Size (n)=72

→P=% of people who listen to radio while they are at work =16 %

→B=1 - P= 100% - 16% =84%

→Standard Deviation when Probability and Sample Size is given

`\sigma=\sqrt{(P(1-P))/(n)}\\\\ \sigma =\sqrt{((16)/(100) * (84)/(100))/(72)}\\\\ \sigma=\sqrt{(1344)/(720,000)}\\\\\sigma=\sqrt{(18.66)/(10000)}\\\\\sigma=(4.320)/(100)\\\\ \sigma=0.0432`

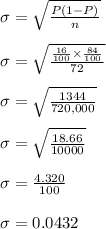
So, standard deviation of the sampling distribution of the proportion for the sample of size 72= 0.0432=0.043 (Approx)