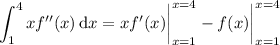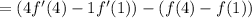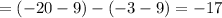Some characters in your question are not displayed properly, so I'm guessing at what it says.
"Suppose that
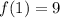
,
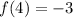
,
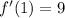
,
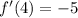
, and

is continuous. Find the value of

."
(Correct me if I'm wrong!)
Integrate by parts, letting

and
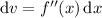
, so that
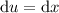
and
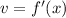
. Then you have
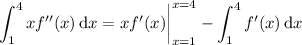
Integrating once more gives