Question

The weight W of an object varies inversely as the square of the distance d from the center of the earth. At sea level​ (3978 mi from the center of the​ earth), an astronaut weighs 129129 lb. Find her weight when she is 144144 mi above the surface of the earth and the spacecraft is not in motion.

Answer 1

`\bf \begin{array}{llllll} \textit{something}&&\textit{varies inversely to}&\textit{something else}\\ \quad \\ \textit{something}&=&\cfrac{{{\textit{some value}}}}{}&\cfrac{}{\textit{something else}}\\ \quad \\ y&=&\cfrac{{{\textit{k}}}}{}&\cfrac{}{x} \\ &&y=\cfrac{{{ k}}}{x} \end{array}`

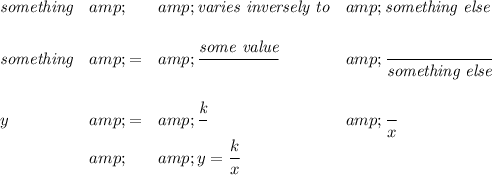
with "k" being the "constant of variation"

so. hmm in this case is "w" inversely varying to the square of the distance or d²

thus
`\bf w=\cfrac{k}{d^2}\qquad \begin{cases} d=3978\\ w=129 \end{cases}\implies 129=\cfrac{k}{3978^2}`

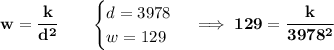
solve for "k", to see what the constant of variation is

and plug it back in
`\bf w=\cfrac{k}{d^2}`

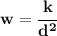
now.. .to find her weight when she's 144miles above the surface, well
that's just
`\bf w=\cfrac{k}{(3978+144)^2}`

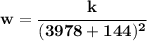
and since you already know what "k" is, just divide and simplify away, to get "w"