Which of the following is a valid conclusion for the problem x2 + 6x + 8 = 0? x - 3 = 0 and x + 5 = 0 x + 4 = 0 and x - 2 = 0 x + 4 = 0 and x + 2 = 0 x - 4 = 0 and x + 2 = 0

Question

asked Dec 26, 2018 29.5k views

2 Answers

Matt Humphrey · Answer 1 · 2018-12-30T18:20:38+0000

Answer:

option (3) is correct.

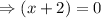$\Rightarrow (x+2)=0$ or
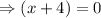
$\Rightarrow (x+4)=0$

Explanation:

Given quadratic equation
x^2+6x+8=0

We have to choose a valid conclusion for the problem
x^2+6x+8=0

Consider the given quadratic equation
.

We can solve the quadratic equation using middle term split,

6x can be written as 2x +4x , thus equation becomes,

x^2+6x+8=0

$\Rightarrow x^2+2x+4x+8=0$

Taking x common from first two term and 4 common from last two terms, we have,

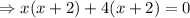
$\Rightarrow x(x+2)+4(x+2)=0$

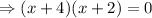
$\Rightarrow (x+4)(x+2)=0$

Using zero product property,
$a\cdot b=0 \Rightarrow a=0 \ or \ b=0$ ,we have,

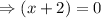$\Rightarrow (x+2)=0$ or
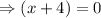
$\Rightarrow (x+4)=0$

Thus, option (3) is correct.