Question

You have a two-wheel trailer that you pull behind your ATV. Two children with a combined mass of 92.2 kg hop on board for a ride through the woods and the springs (one for each wheel) each compress by 5.97 cm. When you pull the trailer over a tree root in the trail, it oscillates with a period of 1.14 s. Determine the force constant of the springs in N/m.

Answer 1

k = 1400.4 N / m

Step-by-step explanation:

When the springs are oscillating a simple harmonic motion is created where the angular velocity is

w² = k / m

w =
`\sqrt{ (k)/(m) }`

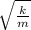
where angular velocity, frequency and period are related

w = 2π f = 2π / T

we substitute

2π / T = \sqrt{ \frac{k}{m} }

T² = 4π²
`(m)/(k)`

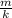
k = π²
`(m)/(T^(2) )`

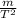
in this case the period is T = 1.14s, the combined mass of the children is

m = 92.2 kg and the constant of the two springs is

k = 4π² 92.2 / 1.14²

k = 2800.8 N / m

to find the constant of each spring let's use the equilibrium condition

F₁ + F₂ - W = 0

k x + k x = W

indicate that the compression of the two springs is the same, so we could replace these subtraction by another with an equivalent cosecant

(k + k) x = W

2k x = W

k_eq = 2k

k = k_eq / 2

k = 2800.8 / 2

k = 1400.4 N / m