Question

A circle is centered at the point (-7, -1) and passes through the point (8, 7).

The radius of the circle is ? units. The point (-15, ?) lies on this circle

Answer 1

Radius = √(7-(-1))² + (8-(-7))² = √8²+15² = √289 = 17

Let the point be (-15,y)
(-15-(-7))² + (y-(-1))² = 17²
⇒ -8² + (y+1)² = 17²
⇒ 64 + (y+1)² = 289
⇒ (y+1)² = 289 - 64 = 225
⇒ y+1 = +15 or -15
⇒ y = +15-1 or -15-1
⇒ y = 14 or -16

Thus, the point can be either (-15,14) or (-15,-16)

Answer 2

Radius of the circle is, 17 units

The point can be either (-15, -16) or (-15, -14)

Explanation:

The general equation of circle is given by:

`(x-h)^2+(y-k)^2 = r^2`

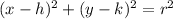
where, r is the radius of the circle and (h, k) is the center of the circle.

As per the statement:

A circle is centered at the point (-7, -1) and passes through the point (8, 7).

⇒Center = (-7, -1)

then;

`(x+7)^2+(y+1)^2 = r^2`

Since, the circle passes through the point (8, 7) then we have;

`(8+7)^2+(7+1)^2 = r^2`

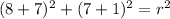
Solve for r:

`15^2+8^2 = r^2`

⇒
`225+64 = r^2`

⇒
`279 = r^2`

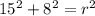
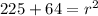
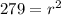
or

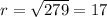`r = √(279) = 17` units

⇒the radius of the circle is, 17 units

It is given that:

The point (-15, y) lies on this circle.

`(x+7)^2+(y+1)^2 =289`

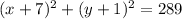
Substitute the value x = -15 and solve for y

`(-15+7)^2+(y+1)^2 =289`

⇒
`(-8)^2+(y+1)^2 = 289`

⇒
`64+(y+1)^2= 289`

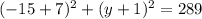
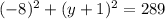
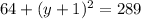
Subtract 64 from both sides we have;

`(y+1)^2 = 225`

⇒
`y+1 = \pm 15`

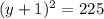
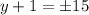
⇒y = -16 or y = -14

Therefore, the point can be either (-15, -16) or (-15, -14)