Question

A farmer wishes to fence a rectangular area behind his barn. The barn forms one end of the rectangle and the length of the rectangle is three times the width. How many linear feet of fence must he buy if the perimeter of the rectangle is 320 feet

Answer 1

Length is 3w
Width is w
So add 3w+3w+w+w.
8w=320
Divide by 8
W=40

Answer 2

280 feet

Explanation:

Let width of rectangle be x

Since we are given that the length of the rectangle is three times the width.

⇒ Length = 3x

Now, perimeter of rectangle =
`2(Length+Width)`

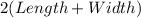
Perimeter of rectangular area:

`320 =2(x+ 3x)`

`320 =2(4x)`

`320 =8x`

`(320)/(8) = x`

`40= x`

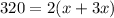
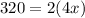
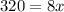
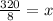
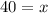
Thus the width of the rectangular area is 40 feet .

Length = 3x= 40*3=120 feet.

Since we are given that The barn forms one end of the rectangle

⇒
`(2* length)+width`

⇒
`(2* 120)+40`

⇒
`240+40`

⇒
`280`

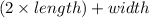
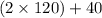
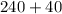
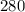
Hence he must buy 280 feet of fence to form barn if the perimeter of the rectangle is 320 feet