Question

Which strategy is the most appropriate to solve : x^2 - 8x = 242 ?

A. Completing the square
B. Zero product property
C. Square root property

Answer 1

A), bring 242 in the equation so you can completely the square.

Answer 2

Answer: The appropriate strategy is (A). Completing the square.

Step-by-step explanation: The given quadratic equation is

`x^2-8x=242.~~~~~~~~~~~~~~~(i)`

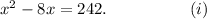
Since the constant term is not equal to zero, so Zero product property is no appropriate to solve the equation.

From equation (i), we have

`x^2-8x=242\\\\\Rightarrow x^2-8x-242=0.`

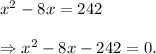
The left hand side of the above equation is not a perfect square, so the square root property is also not appropriate.

Completing the square strategy is appropriate to solve the equation (i).

The solution using this strategy is as follows:

`x^2-8x=242\\\\\Rightarrow x^2-8x+16=242+16\\\\\Rightarrow (x+4)^2=256\\\\\Rightarrow x+4=\pm 16\\\\\Rightarrow x=12, -20.`

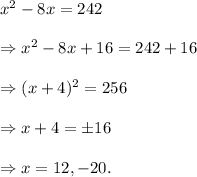
In this way, we can solve the equation by Completing the square strategy.

Thus, (A) is the correct option.