Question

the vertex of a quadratic function is (6,2) and the y-intercept of the function is (0,-70). the equation of the function in vertex form, f (x)=a(x-h)^2+k, is shown. -70=a (0-6)^2+2. what is the value of a?

Answer 1

Well, just solve the equation

-70 =
`a(0-6)^2+2`
-70 =
`a(-6)^2+2`
-70 - 2 = 36a
a = -72/36 = -2

Answer 2

The value of a is -2

Explanation:

In the equation of the quadratic function:

`f(x)=a(x-h)^(2)+k`

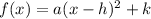
The point (h,k) is the vertex and all the points with the form (x,f(x)) belong to the quadratic functions.

Then, in this case, the point (6,2) is the vertex (h,k) and the y-intercept of the function (0,-70) is a point that follow the form (x,f(x)).

So, if we replace, h by 6, k by 2, x by 0 and f(x) by -70 and we solve for a, we get:

`-70=a(0-6)^(2)+2`

`-70=a(6^(2) )+2\\-70-2=36a\\(-72)/(36) =a\\-2 =a`

Therefore the value of a on the equation is -2.