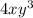Question

What is the greatest common factor of 8xy5−16x2y3+20x4y4

Answer 1

the greatest common factor is 4xy^3

Answer 2

Greatest common factor(GCF) of a polynomial states that the largest polynomial that divides into the polynomials.

Given that:
`8xy^5-16x^2y^3+20x^4y^4`

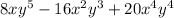
First find the GCF of the expression.

The GCF of 8, 16 and 20 is 4.

The GCF of
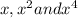`x, x^2 and x^4` is x.

And the

GCF of
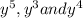`y^5, y^3 and y^4` is
`y^3`

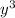
Combine these to find the GCF of the polynomial is,
`4xy^3`

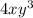
then;

`8xy^5-16x^2y^3+20x^4y^4` =
`4xy^3(2y^2-4x+5x^3y)`

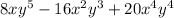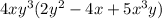
Therefore, the greatest common factor of

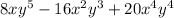`8xy^5-16x^2y^3+20x^4y^4` is
`4xy^3`