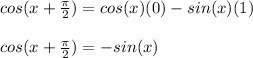Answer:
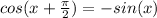
The identity is true
Explanation:
This can be verified using multiple methods, for example you can use graphical methods if you know the exact form of the cosine function and the sine function. However, in this case, we are going to use a very useful identity, which is the cosine sum identity. This identity is given by the following equation:

In this case:

So:
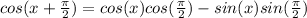
Where:

Therefore: