Question

the mean score of a mathematics placement exam is 125 with a standard deviation of 12.51. those who score i the bottom 20% are required to take a remedial course. assuming the data are not normally distributed, what is the lowest score you can get and not have to take the remedial math class?

Answer 1

You're looking for
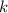
`k` such that


`\mathbb P(X<k)=0.20`

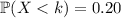
Transforming the standard normal distribution, you have


`\mathbb P(X<k)=\mathbb P\left((X-125)/(12.51)<(k-125)/(12.51)\right)=\mathbb P(Z<k^*)`

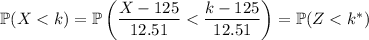
where
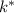
`k^*` is the cutoff score in terms of this new distribution. The z-score corresponding to a probability of 0.20 is approximately
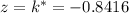
`z=k^*=-0.8416`, which means the cutoff test score is


`k^*=(k-125)/(12.51)\implies k=125+12.51k^*\approx114.47`

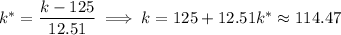
Rounding to the nearest whole point, a score of about 114 is the bare minimum requirement to not have to take the remedial course.