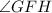Answer:
Option C is correct.
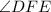 is congruent to
is congruent to
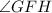
Explanation:
Given:
DG = 12 units, GF = 4 units , EH = 9 units and HF = 3 units
then;
DF = DG +GF = 12+4 = 16 and EF = EH+HF = 9+3 =12
In ΔDFE and ΔGFH
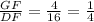
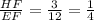
therefore;
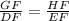
 [angle]
[angle]
By SAS(Side-Angle-Side) Similarity Theorem states that if two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
Therefore, by SAS Similarity theorem;
△DFE
 △GFH
△GFH
Therefore, the only condition is
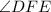 is congruent to
is congruent to