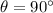Question

What is the maximum of f(x) = sin(x)?

Answer 1

Sinx= 1(maximum value) 

Answer 2

The Maximum value of f(x)=sin(x) is 1 , when
`\theta = 90^(\circ)`

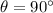
Explanation:

Property of Sine function:

• 
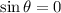  `\sin \theta =0` when
  `\theta = 0^(\circ) ,180^(\circ), 360^(\circ)`

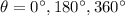
• Maximum value of
  `\sin \theta` is 1 , when
  `\theta = 90^(\circ)`

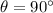
• Minimum value of
  `\sin \theta` is -1 , when
  `\theta = 180^(\circ)`

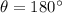
• Range of values of
  `\sin \theta` is
  `-1\leq \sin \theta \leq 1`

Given: f(x) = sin(x)

Then, by the property of sine function:

Maximum value of f(x) is 1 , when
`\theta = 90^(\circ)`