Answer:
5.
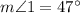
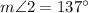
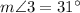
7.

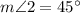
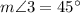
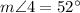
Explanation:
5.
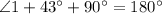
By triangle angle sum theorem
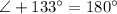
Addition property of integers
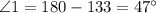
By using subtraction property of equality
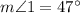
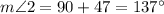
By using exterior angle theorem
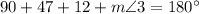
By using triangle angle sum theorem

Addition property of integers

Using subtraction property of equality
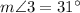
7.We are given that
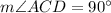
BC bisects angle ACD

Therefore,
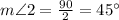
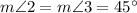
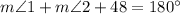
By using triangle angle sum theorem
Substitute the value
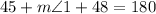
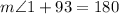
By addition property of integers
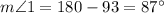
By using subtraction property of equality
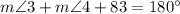
By using triangle angle sum property
Substitute the values

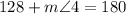
Using addition property of integers

Using subtraction property of equality