[1] An exponential model forces us to use the following formula:

where A is a scaling variable, r is the growth rate, and t is time.
[2] Let's say that "soon" means t is basically 0. We know that the patient has 300 mg of the drug. In our formula, we must have
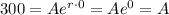
Hey! We just found that A = 300. Cool.
[3] After 2 hours, we are told that only 75 mg is left. In our formula we must have
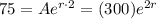
notice that since we know that A = 300 we have plugged that in. We can solve for the unknown r
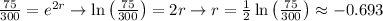
So, now we know that r = -0.693.
[4] Our finished model looks like this
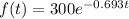
Congrats! You've just built a formula!
[5] To find the amount of aspirin after 4 hours, we use our newly created formula: