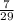Question

Your friend brings 15 chocolate cupcakes and 15 vanilla cupcakes to school. Students will take turns picking a pair of cupcakes at random. What is the probability that the first student will pick 2 chocolate cupcakes?

Answer 1

umm i think it is 1/3 because there are 30 in total and the chances are that you'll either pick
2 vanilla
2 chocolate
1 vanilla and 1 chocolate

Answer 2

Probability says that divide the required possible outcomes by the total number of outcome.

As per the statement:

Your friend brings 15 chocolate cupcakes and 15 vanilla cupcakes to school.

We have to find the probability that the first student will pick 2 chocolate cupcakes.

Number of required possible outcomes =
`^(15)C_(2) * ^(15)C_(0)`

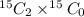
Total number of outcomes =
`^(30)C_(2)`

by definition we have;

`\text{P(2 chocolate cupcakes)} = (^(15)C_(2) * ^(15)C_(0))/(^(30)C_(2))`

We know that:

`^(15)C_(0) = 1`

⇒
`\text{P(2 chocolate cupcakes)} = (^(15)C_(2))/(^(30)C_(2))`

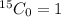
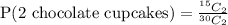
Using the formula:

`^(n)C_(r) = (n!)/(r!(n-r)!)`

⇒
`\text{P(2 chocolate cupcakes)} = ((15!)/(2! \cdot 13!))/((30!)/(2! \cdot 28!))`

⇒
`\text{P(2 chocolate cupcakes)} = ((15 \cdot 14 \cdot 13!)/(2! \cdot 13!))/((30 \cdot 29 \cdot 28!)/(2! \cdot 28!))`

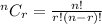
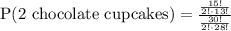
Simplify:

`\text{P(2 chocolate cupcakes)} = (15 \cdot 14)/(30 \cdot 29) = (7)/(29)`

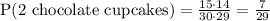
therefore, the probability that the first student will pick 2 chocolate cupcakes is,
`(7)/(29)`