Question

Suppose that X has a discrete uniform distribution on the integers 0 through 9. Determine the mean, variance, and standard deviation of the random variable equals 5x=y

Answer 1

With 10 integers available,
`X` has PMF


`\mathbb P(X=x)=\begin{cases}\frac1{10}&\text{for }0\le x\le9,x\in\mathbb Z\\\\0&\text{otherwise}\end{cases}`

We're interested in the statistics of the new random variable
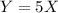
`Y=5X`. To do this, we need to know the PMF for
`Y`. This isn't too hard to find.


`\mathbb P(Y=y)=\mathbb P(5X=y)=\mathbb P\left(X=\frac y5\right)`

Since the PMF for
`X` gives a value of
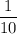
`\frac1{10}` whenever
`x` is an integer between 0 and 9, it follows that
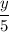
`\frac y5` must also be an integer for the PMF to give the identical value of
`\frac1{10}`. This means


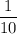
`\mathbb P(Y=y)=\begin{cases}\frac1{10}&\text{for }y\in\{0,5,\ldots,45\}\\\\0&\text{otherwise}\end{cases}`

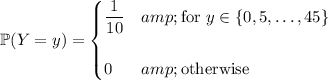
Now the mean (expectation) is


`\mathbb E(Y)=\displaystyle\sum_yy\mathbb P(Y=y)=\frac1{10}\sum_{y\in\{0,\ldots,45\}}y`

`\mathbb E(Y)=(225)/(10)=22.5`

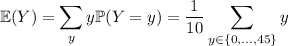
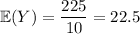
The variance would be


`\mathbb V(X)=\mathbb E(X^2)-\mathbb E(X)^2`

`\mathbb V(X)=\displaystyle\sum_yy^2\mathbb P(Y=y)-\mathbb E(Y)^2`

`\mathbb V(X)=\displaystyle\frac1{10}\sum_{y\in\{0,\ldots,45\}}y^2-\left((225)/(10)\right)^2`

`\mathbb V(X)=(7125)/(10)-(50625)/(100)=206.25`

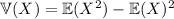
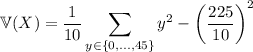
The standard deviation is the square root of the variance, so you have


`√(\mathbb V(X))=√(206.25)\approx14.3614`