Question

Below is the graph of f(x)=In(x). how would you describe the graph of g(x)=1/3In(x)

Answer 1

This is the graph of f(x)=ln(x)

Answer 2

The g(x) represent the vertical compression by a factor of
`(1)/(3)`

Explanation:

Given : The graph of
`f(x)=\ln (x)`

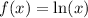
To find : How would you describe the graph of
`g(x)=(1)/(3) \ln (x)`

Solution :

The functions are :

`f(x)=\ln (x)`

`g(x)=(1)/(3) \ln (x)`

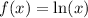
g(x) is in the form of,

`g(x)=kf(x)`

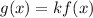
Where, k is stretch factor.

If k>1, then it represents vertical stretch

If k<1, then it represents vertical compression.

We know,

`k=(1)/(3)=0.3<1`

The g(x) represent the vertical compression by a factor of
`(1)/(3)`

We plot the graph of both the functions.

Refer the attached graph below.