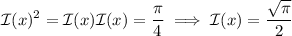Question

Express (1/2)! in terms of pi.

Answer 1

Since


`n!=\Gamma(n+1)=\displaystyle\int_0^\infty t^ne^(-t)\,\mathrm dt`

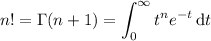
you have


`\left(\frac12\right)!=\displaystyle\int_0^\infty t^(1/2)e^(-t)\,\mathrm dt`

Let
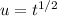
`u=t^(1/2)`, so that
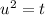
`u^2=t` and
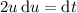
`2u\,\mathrm du=\mathrm dt`. This means the integral is equivalent to


`\displaystyle2\int_0^\infty u^2e^(-u^2)\,\mathrm du`

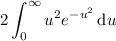
Integrating by parts, setting
`f=u`,
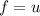
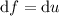
`\mathrm df=\mathrm du` and
`\mathrm dg=ue^(-u^2)\,\mathrm du`,
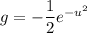
`g=-\frac12e^(-u^2)` yields


`\displaystyle2\int_0^\infty u^2e^(-u^2)\,\mathrm du=2\left(-\frac12ue^(-u^2)\bigg|_(u=0)^(u\to\infty)+\frac12\int_0^\infty e^(-u^2)\,\mathrm du\right)=\int_0^\infty e^(-u^2)\,\mathrm du`

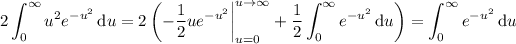
You might already know that the value of this integral is
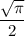
`\frac{\sqrt\pi}2`, so you're done. Or, if you're not familiar, you can derive this result.

If
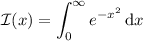
`\mathcal I(x)=\displaystyle\int_0^\infty e^(-x^2)\,\mathrm dx`, then you have


`\displaystyle\mathcal I(x)\mathcal I(y)=\left(\int_0^\infty e^(-x^2)\,\mathrm dx\right)\left(\int_0^\infty e^(-y^2)\,\mathrm dy\right)=\int_0^\infty\int_0^\infty e^(-(x^2+y^2))\,\mathrm dx\,\mathrm dy`

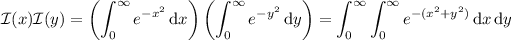
Converting to polar coordinates yields


`\displaystyle\int_0^(\pi/2)\int_0^\infty re^(-r^2)\,\mathrm dr\,\mathrm d\theta=\frac\pi2\int_0^\infty re^(-r^2)\,\mathrm dr=\frac\pi4`

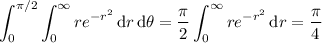
and so


`\displaystyle\mathcal I(x)^2=\mathcal I(x)\mathcal I(x)=\frac\pi4\implies \mathcal I(x)=\frac{\sqrt\pi}2`