Question

How will the solution of the system y > 2x and y < 2x change if the inequality sign on both inequalities is reversed to y < 2x and?

Answer 1

There is no solution to the system in its original form. There are no points in common. If the signs are reversed, the system has an intersection with an infinite number of solutions.

Explanation:

Answer 2

There is no change in the solution set of both system of inequalities. Both system of inequalities have no solution.

Explanation:

The system of inequality is

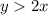`y>2x` ....(1)

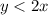`y<2x` .....(2)

The related equation of both inequality are same, i.e.,

`y=2x`

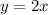
The sign of inequalities are ">" and "<" , so the point on the related line are not included in the solution set. The shaded region of first inequality is above the line and the shaded region of second inequality is above the line.

It means there is no solution of the given system of inequality.

If the inequality sign on both inequalities is reversed, then the new system of inequalities is

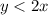`y<2x` ....(3)

It is same as inequality (2).

`y>2x`

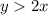
It is same as inequality (1).

Both system of inequalities are same, therefore the new system of inequality has no solution.

Therefore there is no change in the solution set of both system of inequalities. Both system of inequalities have no solution.