Question

Which of the following values would be obtained using 5 midpoint rectangles of equal width to estimate the integral from 0 to 1 of x squared, dx?

Answer 1

Partition the interval [0,1] as


`\left[0,\frac15\right]\cup\left[\frac15,\frac25\right]\cup\left[\frac25,\frac35\right]\cup\left[\frac35,\frac45\right]\cup\left[\frac45,5\right]`

The midpoints of the intervals are, respectively
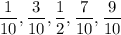
`\frac1{10},\frac3{10},\frac12,\frac7{10},\frac9{10}` - these are your sample points.

The integral is approximated by


`\displaystyle\int_0^1x^2\,\mathrm dx\approx\sum_(n=1)^5f(x_n)\Delta x`

where
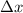
`\Delta x` is the difference between the partition endpoints, i.e.
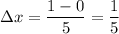
`\Delta x=\frac{1-0}5=\frac15`, and
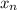
`x_n` is the midpoint of the
`n`th partition. You have


`\displaystyle\sum_(n=1)^5f(x_n)\Delta x=\frac15\left(\left(\frac1{10}\right)^2+\left(\frac3{10}\right)^2+\left(\frac12\right)^2+\left(\frac7{10}\right)^2+\left(\frac9{10}\right)^2\right)=(33)/(100)`

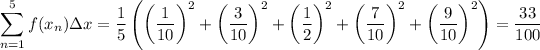
For comparison, the actual value of the integral is
`\frac13`, so the approximation is valid to two decimal places.