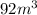The figure is a sphere with a cone within it. To the nearest whole number, what is the approximate volume of the shaded part of this figure? Use 3.14 for Pi. Drag the correct va…

Question

asked Jan 9, 2018 72.8k views

2 Answers

Vishnu Ranganathan · Answer 1 · 2018-01-14T19:32:13+0000

92 m³

First we are going to find the volumes of the sphere and cone separately; then, we'll subtract the volume of the cone from the volume of the sphere.

Volume of the sphere:

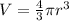
$V=(4)/(3) \pi r^3$

where

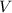is the volume of the sphere

is the radius

We can infer from our picture that r = 3 m, so let's replace the value

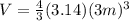
V=(4)/(3) (3.14) (3m)^3

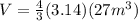
V=(4)/(3) (3.14) (27m^3)

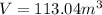
V=113.04m^3

Volume of the cone:

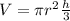
$V=\pi r^2(h)/(3)$

where

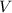is the volume of the cone

is the radius

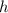is the height

We can infer from our picture that r = 2 m and h = 5 m, so let's replace the values

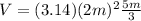
V=(3.14)(2m)^2(5m)/(3)

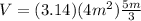
V=(3.14)(4m^2)(5m)/(3)

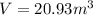
V=20.93m^3

Volume of the shaded area = volume of the sphere - volume of the cone

Volume of the shaded area =
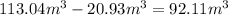
113.04m^3-20.93m^3=92.11m^3

And rounded to the nearest integer:

Volume of the shaded area =
92m^3