Question

The sound intensity of a typical vacuum cleaner is 80 dB (decibels). Sound intensity of 160 dB will burst an eardrum. How many times louder is the sound that will burst an eardrum than the sound of a vacuum cleaner?

Answer 1

Ten thousand times as loud.

Answer 2

Using logarithmic rule:

`\log (m)/(n) = \log m -\log n`

`\log_b b^a = a`

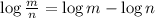
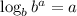
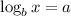`\log_b x = a` then
`x = b^a`

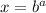
Given that,

Sound intensity of a typical vacuum cleaner = 80 dB

Sound intensity of burst of eardrum = 160 dB

Let, I₁ and I₂ b e the intensity of typical vacuum and intensity of eardrum.

Use the formula:

`1 dB = 10\log_(10) ((I)/(I_0))`

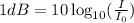
As per the statement

The sound intensity of a typical vacuum cleaner is 80 dB (decibels).

⇒
`80 dB= 10\log_(10) ((I_1)/(10^(-12)))`

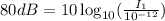
Divide both sides by 10 we have;

`8 dB= \log_(10) ((I_1)/(10^(-12)))`

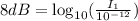
Apply the logarithmic rules:

then;

`8 = \log_(10) I_1 - \log_(10) 10^(-12)`

⇒
`8 = \log_(10) I_1 + 12`

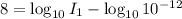
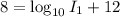
Subtract 12 from both sides we have;

`-4= \log_(10) I_1`

⇒
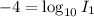
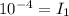`10^(-4) = I_1` ......[A}

It is also given that: Sound intensity of 160 dB will burst an eardrum.

⇒
`160 dB= 10\log_(10) ((I_2)/(10^(-12)))`

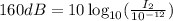
Divide both sides by 10 we have;

`16 dB= \log_(10) ((I_2)/(10^(-12)))`

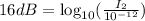
Apply the logarithmic rules:

`16 = \log_(10) I_2 - \log_(10) 10^(-12)`

⇒
`16 = \log_(10) I_2 + 12`

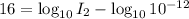
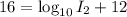
Subtract 12 from both sides we have;

⇒
`4 = \log_(10) I_2`

⇒
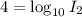
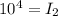`10^(4) = I_2` ......[B]

We have to find how many times louder is the sound that will burst an eardrum than the sound of a vacuum cleaner.

`(I_2)/(I_1) = (10^4)/(10^(-4)) = 10^8`

⇒
`I_2 = 10^8 * I_1`

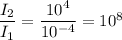
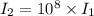
Therefore,
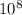`10^8` times louder is the sound that will burst an eardrum than the sound of a vacuum cleaner