Question

Justin deposits $8,000 in a one-year CD at 3.1% interest, compounded daily. What is Justin’s annual percentage yield (APY) to the nearest hundredth of a percent? (Hint: Find the interest using the compounding formula. Then use the simple interest formula to find the rate, as if the interest you found at first were simple interest.)

Answer 1

Total = Princ * (1 +rate/365)^365*1 year
Total = 8,000 * (1 + .031/365)^365
Total = 8,000 * (1.000084931506849315)^365
Total = 8,000 * 1.0314841461
Total = 8,251.87

rate = (1 + .031/365)^365 = 1.0314841461 =
3.14841461

Answer 2

Justin’s annual percentage yield = 3.15%

Explanation:

Justin deposits $8,000 in a one-year CD at 3.1% interest, compounded daily.

WE apply compound interest formula

`A=P (1+(r)/(n) )^(t*n)`

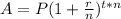
P is the initial amount deposited= 8000

r is the rate of interest = 3.1% = 0.031

n is the number of periods compounded = 365

t is the number of years = 1

Plug in all the values and find out A

`A=8000 (1+(0.031)/(365) )^(1*365)`

A=8000 * (1.000084931506849315)^365

A= 8251.87

Interest amount = 8251.87 - 8000= $251.87

To find annual percentage yield we use simple interest formula

Interest = P*r*t

251.87 = 8000* r * 1

Divide by 8000 on both sides

r =0.0314838

To find out the percentage we multiply by 100

r =0.0314838 * 100 = 3.14838

Its approximately 3.15%