Question

According to the Rational Root Theorem, the following are potential roots of f(x) = 6x^4 + 5x^3 – 33x^2 – 12x + 20.

-5/2, -2, 1, 10/3

Which is an actual root of f(x)?
A. -5/2
B. –2
C. 1
D. 10/3

Answer 1

A graphical analysis of this function indicates that out of those possible roots, -5/2 is the only true root

Answer 2

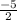`(-5)/(2)` Option A

Explanation:

Given that a function,

f(x) = 6x⁴ + 5x³ - 33x² - 12x + 20

put the numbers in place of x, if function become 0 it means that number is root of the given function.

For
`(-5)/(2)`

`f((-5)/(2))=6((-5)/(2))^(4)+5((-5)/(2))^(3)-33((-5)/(2))^(2)-12((-5)/(2))+20`

`f((-5)/(2))=0`

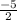
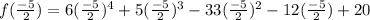
So,
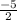`(-5)/(2)` is the root of given function.

That's the final answer.