How to find the limit \lim_(n \to \infty) (1)/(n^(k+1)) (k!+ ((k+1)!)/(1!) +...+((k+n)!)/(n!)), ~~~k\in N

Question

How to find the limit


`\lim_(n \to \infty) (1)/(n^(k+1)) (k!+ ((k+1)!)/(1!) +...+((k+n)!)/(n!)), ~~~k\in N`

Answer 1

`\displaystyle\lim_(n\to\infty)\left(k!+((k+1)!)/(1!)+\cdots+((k+n)!)/(n!)\right)=\lim_(n\to\infty)(\displaystyle\sum_(i=0)^n((k+i)!)/(i!))/(n^(k+1))=\lim_(n\to\infty)(a_n)/(b_n)`

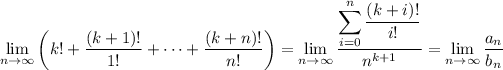
By the Stolz-Cesaro theorem, this limit exists if


`\displaystyle\lim_(n\to\infty)(a_(n+1)-a_n)/(b_(n+1)-b_n)`

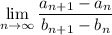
also exists, and the limits would be equal. The theorem requires that
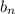
`b_n` be strictly monotone and divergent, which is the case since
`k\in\mathbb N`.

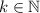
You have


`a_(n+1)-a_n=\displaystyle\sum_(i=0)^(n+1)((k+i)!)/(i!)-\sum_(i=0)^n((k+i)!)/(i!)=((k+n+1)!)/((n+1)!)`

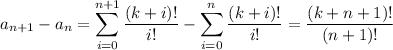
so we're left with computing


`\displaystyle\lim_(n\to\infty)((k+n+1)!)/((n+1)!\left((n+1)^(k+1)-n^(k+1)\right))`

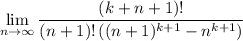
This can be done with the help of Stirling's approximation, which says that for large
`n`,
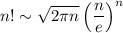
`n!\sim√(2\pi n)\left(\frac ne\right)^n`. By this reasoning our limit is


`\displaystyle\lim_(n\to\infty)\frac{√(2\pi(k+n+1))\left(\frac{k+n+1}e\right)^(k+n+1)}{√(2\pi(n+1))\left(\frac{n+1}e\right)^(n+1)\left((n+1)^(k+1)-n^(k+1)\right)}`

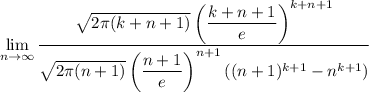
Let's examine this limit in parts. First,


`(√(2\pi(k+n+1)))/(√(2\pi(n+1)))=\sqrt{(k+n+1)/(n+1)}=\sqrt{1+\frac k{n+1}}`

As
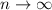
`n\to\infty`, this term approaches 1.

Next,


`\frac{\left(\frac{k+n+1}e\right)^(k+n+1)}{\left(\frac{n+1}e\right)^(n+1)}=(k+n+1)^k\left((k+n+1)/(n+1)\right)^(n+1)=e^(-k)(k+n+1)^k\left(1+\frac k{n+1}\right)^(n+1)`

The term on the right approaches
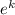
`e^k`, cancelling the
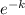
`e^(-k)`. So we're left with


`\displaystyle\lim_(n\to\infty)((k+n+1)^k)/((n+1)^(k+1)-n^(k+1))`

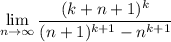
Expand the numerator and denominator, and just examine the first few leading terms and their coefficients.


`\displaystyle((k+n+1)^k)/((n+1)^(k+1)-n^(k+1))=(n^k+\cdots+(k+1)^k)/(n^(k+1)+(k+1)n^k+\cdots+1+n^(k+1))=(n^k+\cdots+(k+1)^k)/((k+1)n^k+\cdots+1)`

Divide through the numerator and denominator by
`n^k`:


`(n^k+\cdots+(k+1)^k)/((k+1)n^k+\cdots+1)=\frac{1+\cdots+\left(\frac{k+1}n\right)^k}{(k+1)+\cdots+\frac1{n^k}}`

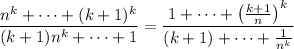
So you can see that, by comparison, we have


`\displaystyle\lim_(n\to\infty)((k+n+1)^k)/((n+1)^(k+1)-n^(k+1))=\lim_(n\to\infty)\frac1{k+1}=\frac1{k+1}`

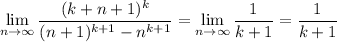
so this is the value of the limit.