Question

Which smallest number will have 15,20,25,31 nd 43 as reminder respectively when divided by 20, 25, 30, 36,48

please explain the answer you found

Answer 1

I assume by smallest number, you're really looking for the smallest *positive* number.

Notice that -5 fits all these requirements:


`-5\equiv15\mod20`

`-5\equiv20\mod25`

`-5\equiv25\mod30`

`-5\equiv31\mod36`

`-5\equiv43\mod48`

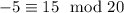
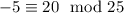
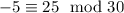
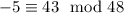
Any number of the form
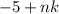
`-5+nk` will also satisfy these conditions, where
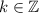
`k\in\mathbb Z` and
`n` is the least common multiple of the moduli. You have


`\mathrm{lcm}(20,25,30,36,48)=3600`

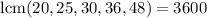
so the least positive number would be achieved with
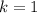
`k=1`, giving 3595 as the answer. (Verified with a script.)