Question

why polar coordinates seem better suited for circular-type functions, while the rectangular coordinate system seems better suited for linear-type graphs.

Answer 1

Because "circular-type" functions can be more easily described by the periodic functions
`\sin` and
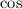
`\cos`, which are deeply involved in the behavior of "circular-type" functions. Also, using a polar coordinate plane allows you to draw graphs of equations that typically aren't functions.

For example, the unit circle requires two equations to be graphed to fully represent the circle in the rectangular coordinate plane.


`x^2+y^2=1\implies y=\pm√(1-x^2)`

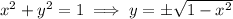
On the other hand, in polar coordinates, substituting
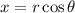
`x=r\cos\theta` and
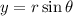
`y=r\sin\theta` reduces this to a constant function,


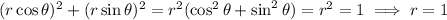
`(r\cos\theta)^2+(r\sin\theta)^2=r^2(\cos^2\theta+\sin^2\theta)=r^2=1\implies r=1` (since by definition,
`r\ge0`)