Question

The volume of a sphere is 4,000π m3. What is the surface area of the sphere to the nearest square meter? 181 m2 50,265 m2 2,614 m2 1,307 m2

Answer 1

Volume of a sphere = 4/3 πr³
4/3 * 3.14 * r³ = 4000
4.19 * r³ = 4000
r³ = 4000 / 4.19
r = ∛1058
r = 10.19

Now, surface area = 4πr² = 4 * 3.14 * (10.19)²
S.A. = 12.56 * 104
S.A. = 1307

In short, Your Answer would be Option D) 1307 m²

Hope this helps!

Answer 2

`2614\text{ m}^2`

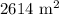
Explanation:

We have been given that the volume of a sphere is
`4,000\pi\text{ m}^3`. We are asked to find the surface area of the sphere.

We will use volume of sphere formula to solve for the radius of sphere as:

`\text{Volume of sphere}=(4)/(3)\pi r^3`

`4,000\pi\text{ m}^3=(4)/(3)\pi r^3`

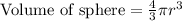
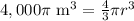
Multiplying both sides by
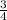`(3)/(4)`, we will get:

`(3)/(4)*4,000\pi\text{ m}^3=(4)/(3)*(3)/(4)*\pi r^3`

`3,000\pi \text{ m}^3=\pi r^3`

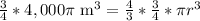
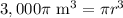
Now, we will divide both sides of our equation by pi.

`\frac{3,000\pi\text{ m}^3}{\pi}=(\pi r^3)/(\pi)`

`3,000\text{ m}^3=r^3`

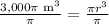
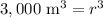
Taking cube root of both sides we will get,

`\sqrt[3]{3,000\text{ m}^3}=r`

`10\sqrt[3]{3}\text{ m}=r`

Now, substituting
`r=10\sqrt[3]{3}\text{ m}` in surface area of sphere formula, we will get,

`\text{Surface area of sphere}=4\pi r^2`

`\text{Surface area of sphere}=4\pi (10\sqrt[3]{3}\text{ m})^2`

`\text{Surface area of sphere}=4\pi*208.0083823051904115\text{ m}^2`

`\text{Surface area of sphere}=2613.9104229\text{ m}^2\approx 2614\text{ m}^2`

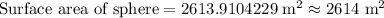
Therefore, option D is the correct choice.