Question

30 POINTS!!!!!!

The population of a local species of beetle can be found using an infinite geometric series where a1 = 960 and the common ratio is one fourth. Write the sum in sigma notation, and calculate the sum (if possible) that will be the upper limit of this population.

Answer 1

Answer: The sum that will be the upper limit of this population is 1280.

Explanation:

Since we have given that

Initial population a₁ = 960

Common ratio =
`(1)/(4)`

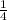
So, We have to write the sum in sigma notation:

`\sum (ar^(n-1))\\\\=\sum 960((1)/(4))^(n-1)\\\\`

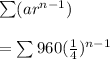
Since
`r=(1)/(4)<1`

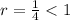
so, the sum is convergent, then,

`\sum 960((1)/(4))^(n-1)=(a)/(1-r)=(960)/(1-(1)/(4))=(960)/((3)/(4))=(960* 4)/(3)=320* 4=1280`

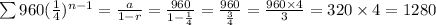
Hence, the sum that will be the upper limit of this population is 1280.

Answer 2

Answer with explanation:

→Infinite Geometric Series

`a_(1)=960\\\\r=(1)/(4)`

→The geometric series having common ratio r, and first term a,can be written as:
`a, ar,ar^2,ar^3,ar^4,.......`

→So, the geometric Series can be Written as:

`960, 960 *(1)/(4),960*[(1)/(4)]^2,960*[(1)/(4)]^3,......\\\\ 960,240,60,15,.....`

→Sum of Infinite geometric Series

=960+240+60+15+.......

`={S_{\text{Infinity}}=\sum_(n=1)^(\infty )960*r^(n-1)=(a)/(1-r)`

`=(960)/(1-(1)/(4))\\\\=(960*4)/(3)\\\\=320*4=1280\\\\=(a)/(1-r)`

Sum ,to infinity, Which is upper limit of this population=1280