Answer:
Part a)
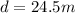
Part b)
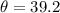 degree East of South
degree East of South
Step-by-step explanation:
Let they both are at origin initially
so here we will have final coordinates of both of them is given as
Ricardo walk 28 m in direction of 60 degree West of North




Jane walks 10 m in direction 30 degree South of West

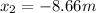


Part a)
distance between them is given as
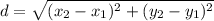
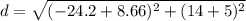
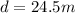
Part b)
direction of motion of Ricardo is given as
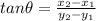
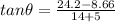
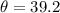 degree East of South
degree East of South