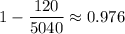Question

A pedlock has a four digit code that includes digits from 0 to 9, inclusive.

What is the probability that the code does not consist of all odd digits of the same digit is not used more than once in the code ??

Answer 1

The answer is 4,920 out of 5,040 or 41/42.

Hope it helps!

Answer 2

There are
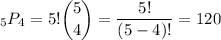
`{}_5P_4=5!\dbinom54=(5!)/((5-4)!)=120` ways of making four-digit codes from the five available odd numerals (1, 3, 5, 7, 9) without replacement. Without any restrictions aside from no replacement, there are
`{}_(10)P_4=10!\dbinom{10}4=(10!)/((10-4)!)=5040` possible codes that can be made. So the probability of randomly choosing a code made up only odd digits is


`(120)/(5040)`

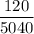
which means the probability of this not occurring is


`1-(120)/(5040)\approx0.976`