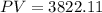Question

An annuity immediate has a first payment of 200 and increases by 100 each year until payments reach 600. there are 5 further payments of 600. find the present value at 5.5%. solution

Answer 1

I will be using present value notation of "v", where v is present value of 1 a year from now.

`v = (1)/(1+i)`
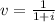
The series of payments looks like this:

`PV = 200 + 300v+400v^2+500v^3 +600v^4+600v^5 +...600v^9`
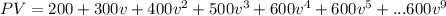
The first 5 payments form an increasing annuity, the last 5 form a standard constant annuity. The increasing part needs to be of the form 1,2,3...n. Since we have 2,3,4,5,6, subtract 1 from each term ---> (1,1,1,1,1) + (1,2,3,4,5).
Rearranging the equation gives:

`PV = 100(1+v+v^2+v^3+v^4) +100(1+2v+3v^2+4v^3+5v^4) \\ +600v^5(1+v+v^2+v^3+v^4)`

Now plugging in the sum formulas for geometric series and increasing series:

`PV = 100((1-v^5)/(1-v)) +100(((1-v^5)/(1-v)-5v^5)/(iv)) +600v^5((1-v^5)/(1-v))`
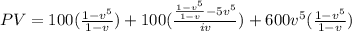
Finally sub in values using i = 5.5% = .055

`PV = 3822.11`