Question

Can you always use synthetic division for dividing polynomials? Explain.

Answer 1

I would say yes.

Typically synthetic division is taught to make it seem like the algorithm only works for rational functions of the form
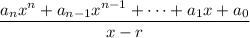
`(a_nx^n+a_(n-1)x^(n-1)+\cdots+a_1x+a_0)/(x-r)`, i.e. only when the divisor
`x-r` is a monic linear polynomial.

However there are expanded algorithms that would allow for division of something like
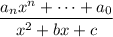
`(a_nx^n+\cdots+a_0)/(x^2+bx+c)` (dividing by higher order monic polynomials) as well as
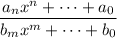
`(a_nx^n+\cdots+a_0)/(b_mx^m+\cdots+b_0)` (dividing by any higher order polynomial provided that
`m\le n`).

Consult the Wiki page on "synthetic division" for more info.