Question

Suppose f(x) and g(x) are differentiable functions with the known values:

X: 0,1,2,3,4
f(x): 1,2,1,0,3
g(x): 5,3,4,2,1
f'(x): 0,2,3,6,1
g'(x): 2,3,4,4,5
(please note this is suppose to be a table so the each number is in a row vertically)

Showing calculations, evaluate the following:
a). d/dx [f(x)/x^2] when x=2
b). d/dx [g(f(x))] when x=3
c). d/dx [sqrt g(x)-1] when x=0

Answer 1

remember the rules
the deritivive of f(g(x))=f'(g(x))g'(x)
and division thing
the deritivieve of f(x)/g(x)=(f'(x)g(x)-g'(x)f(x))/(g(x)^2)
for ax^n, the deritivive is anx^(n-1)
so

a. f(x)/x^2, deritivive is (f'(x)x^2-2xf(x))/(x^4)
for x=2
(f'(2)(2)^2-2(2)f(2))/(2^4)=(2*4-4*1)/16=(8-4)/16=4/16=1/4

b. g(f(x))=g'(f(x))f'(x) at x=3
g'(f(3))f'(3)=g'(0)(3)=(2)(3)=6

c. (g(x)-1)^(1/2)=(1/2)(g(x)-1)^(-1/2)(g'(x))=
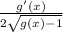
`(g'(x))/(2 √(g(x)-1) )` at x=0

`(g'(0))/(2 √(g(0)-1) )`=
`(2)/(2 √(5-1) )`=
`(2)/(2 √(4) )`=
`(2)/(2(2) )`=
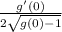
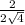
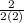
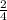
`(2)/(4)`=1/2