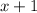Question

What is the oblique asymptote of the function f(x) = the quantity x squared plus 5x plus 6 over the quantity x plus 4?

Answer 1

`f(x)=(x^2+5x+6)/(x+4)=x+1+\frac2{x+4}`

As
`x\to\pm\infty`, the remainder term disappears, so the oblique asymptote is the line
`y=x+1`.

Answer 2

`x+1`

Explanation:

A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.

To find the slant asymptote you must divide the numerator by the denominator using either long division or synthetic division.

We are given a function:

`f(x)=(x^2+5x+6)/(x+4)`

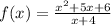
Since in the given function the polynomial in the numerator is a higher degree than the polynomial in the denominator.

So, now to find oblique asymptote we will divide the numerator by the denominator

So, on dividing we get :

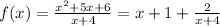`f(x)=(x^2+5x+6)/(x+4)=x+1+\frac2{x+4}`j

Now, As
`x\to\pm\infty` the remainder term disappears

So the oblique asymptote is the line
`y=x+1`

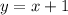
Thus, the oblique asymptote of the function
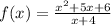`f(x)=(x^2+5x+6)/(x+4)` is
`x+1`