Question

Consider the following game. There is a bottle with 20 colored chips inside. There are 2 blue chips, 4 purple chips, 7 green chips, and 7 red chips. You pay $2 and pick one out at random. If you pick a blue chip, you get a prize of $10. If you pick a purple chip, you get a prize of $5. You get nothing for red or green chips. What is the expected value of playing the game?

Answer 1

Answer: $0

Explanation:

Given : Total colored chips in the bottle= 20

No. of blue chips = 2

Probability of getting blue chip=
`(2)/(20)=0.1`

Prize for blue chip = $10

No. of purple chips = 4

Probability of getting purple chip=
`(4)/(20)=0.2`

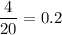
Prize for purple chips = $5

No. of green chips = 7

No.of red chips = 7

Probability of getting green chip or red chip=
`(7+7)/(20)=0.7`

Price for green or red chip = 0

Amount you paid to play the game = $2

Then , the expected value of playing the game will be :-

`0.1*\$10+0.2*\$5+0.7*\$0-\$2\\\\=\$1+\$1-\$2=\$0`

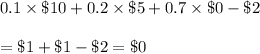
Hence, the expected value of playing the game = $0

Answer 2

Answer: Expected value of playing the game is $0.

Explanation:

Since we have given that

Total number of colored chips = 20

Number of blue chips = 2

Number of purple chips = 4

Number of green chips = 7

Number of red chips = 7

Amount of prize he gets for blue chip = $10

Amount of prize he gets for a purple chip = $5

No amount is given for red or green

Amount he had to pay = $2

So, Expected value of playing the game is given by

`(2)/(20)* 10+(4)/(20)* 5+7* 0+7* 0-2\\\\=1+1-2\\\\=2-2\\\\=\$0`

Hence, Expected value of playing the game is $0.