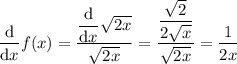Question

What is the domain and derivative of f(x)=ln(2x/sqrt{2 x})?

Answer 1

`\ln x` is defined for
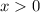
`x>0`, so for
`\ln(2x)/(√(2x))` to be defined, you have to require
`(2x)/(√(2x))>0`.

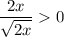
Since
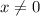
`x\\eq0` in this interval, you can simplify the argument slightly:

`(2x)/(√(2x))=(2x)/(\sqrt2\sqrt x)=\sqrt2\sqrt x=√(2x)`

This means
`f(x)` will be defined whenever
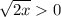
`√(2x)>0`, and this happens for all positive
`x`.

Computing the derivative is an exercise in applying the chain rule:

`(\mathrm d)/(\mathrm dx)f(x)=((\mathrm d)/(\mathrm dx)√(2x))/(√(2x))=((\sqrt2)/(2\sqrt x))/(√(2x))=\frac1{2x}`