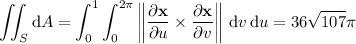Question

Find the surface area of that part of the plane 9x 5y z=5 that lies inside the elliptic cylinder x216 y281=1

Answer 1

I assume the equation of the plane is
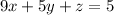
`9x+5y+z=5` and the cylinder has equation
`(x^2)/(16)+(y^2)/(81)=1`.

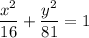
I don't know what techniques are available to you, so I'll resort to (in my opinion) the most reliable: surface integration.

The surface of intersection
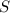
`S` is an ellipse in three dimensional space which can be parameterized by
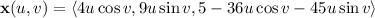
`\mathbf x(u,v)=\langle 4u\cos v,9u\sin v,5-36u\cos v-45 u\sin v\rangle`, with
`u\in[0,1]` and
`v\in[0,2\pi]`.

The area is then given by the integral

`\displaystyle\iint_S\mathrm dA=\int_0^1\int_0^(2\pi)\left\|(\partial\mathbf x)/(\partial u)*(\partial\mathbf x)/(\partial v)\right\|\,\mathrm dv\,\mathrm du=36√(107)\pi`