Question

The function f(x)=60(1.5)xf(x)=60(1.5)x models an animal population after x years.

How does the average rate of change between Years 3 and 6 compare to the average rate of change between Years 0 and 3?

The average rate of change is 1.5 times as fast.

The average rate of change is 3 times as fast.

The average rate of change is 3.375 times as fast.

The average rate of change is 2.25 times as fast.

Answer 1

C.The average rate of change is 3.375 times as fast.You add them up and subract

Answer 2

The average rate of change is 3.375 times as fast.

Explanation:

The given function is
`f(x)=60(1.5)^x`

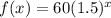
The average rate of change of a function f(x) is given by

`(f(b)-f(a))/(b-a)`

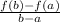
Thus, average rate of change between Years 3 and 6 is given by

`(f(6)-f(3))/(6-3)\\\\=(\left(60\left(1.5\right)^6-60\left(1.5\right)^3\right))/(3)\\\\=160.3125`

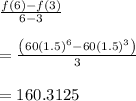
Now, average rate of change between Years 0 and 3

`(f(3)-f(0))/(3-0)\\\\(\left(60\left(1.5\right)^3-60\left(1.5\right)^0\right))/(3)\\\\=47.5`

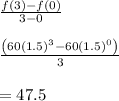
The ratio of these average rate of change is given by

`=(160.3125)/(47.5)\\\\=3.375`

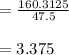
Therefore, the average rate of change is 3.375 times as fast.