Question

I don't exactly understand the question but I need help please.
74 points to best answer

Answer 1

Given triangle GHI with G(4,-3), H(-4,2), and I(2,4), find the perpendicular bisector of HI in standard form.


so first we need to find the midpoint of HI and then find the line perpendicular to it

remember
midpoint formula is
`( (x_1+x_2)/(2) (y_1+y_2)/(2) )`
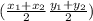
perpendicular lines have slopes that multiply to -1
the equation of a line that passes through the point (x1,y1) and has a slope of m is y-y1=m(x-x1)

so


HI is (-4,2) and (2,4)
find midpoint


`( (-4+2)/(2) (2+4)/(2) )`

`( (-2)/(2) (6)/(2) )`
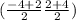
(-1,3)
hmm
the perpendicular bisector is perpendicular to HI
the slope of HI is the slope between (-4,2) and (2,4)
slope=(4-2)/(2-(-4))=2/(2+4)=2/6=1/3
perpendicular to it multiplies to -1
1/3 timeswhat=-1
what=-3

so we know that
the slope is -3 and the point is (-1,3)
y-3=-3(x-(-1))
y-3=-3(x+1)
y-3=-3x-3
y=-3x

the equation is y=-3x

Answer 2

CASE CLOSED
She figured it out on her own ,:D