Question

A campground owner plans to enclose a rectangular field adjacent to a river. the owner wants the field to contain 180,000 square meters. no fencing is required along the river. what dimensions will use the least amount of fencing?

Answer 1

Calling x and y the two sizes of the rectangular field, the problem consists in finding the minimum values of x and y that give an area of
`A=180000 m^2`.
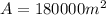
The area is the product between the two sizes:

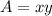
`A=xy` (1)
While the perimeter is twice the sum of the two sizes:

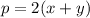
`p=2(x+y)` (2)

From (1) we can write

`y= (A)/(x)`
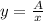
and we can substitute it into (2):

`p=2(x+ (A)/(x))=2x+2 (A)/(x)`

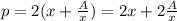
To find the minimum value of the perimeter, we have to calculate its derivative and put it equal to zero:

`p'(x)=0`
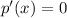
The derivative of the perimeter is

`p'(x) = 2 -2 (A)/(x^2)= (2x^2-2A)/(x^2)`
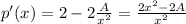
If we require p'(x)=0, we find

`x^2=A`

`x= √(A) = √(180000 m^2)=424.26 m`
And the other side is

`y= (A)/(x)= (180000 m^2)/(424.26 m) =424.26 m`

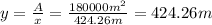
This means that the dimensions that require the minimum amoutn of fencing are (424.26 m, 424.26 m), so it corresponds to a square field.